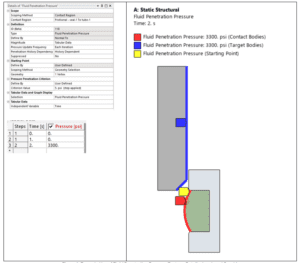
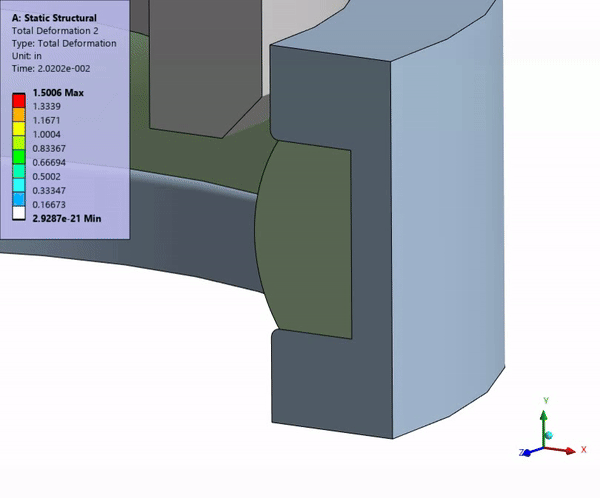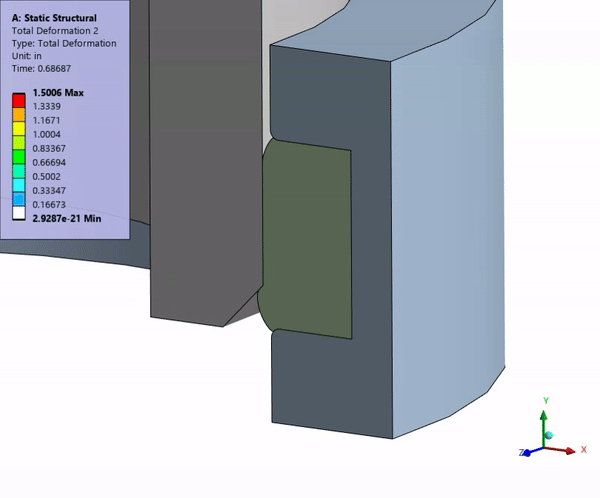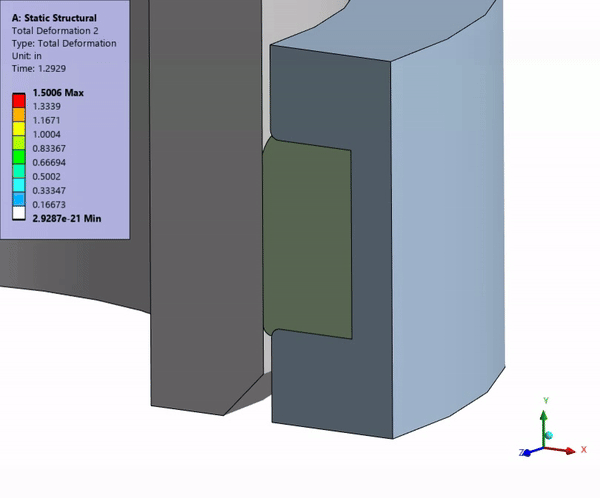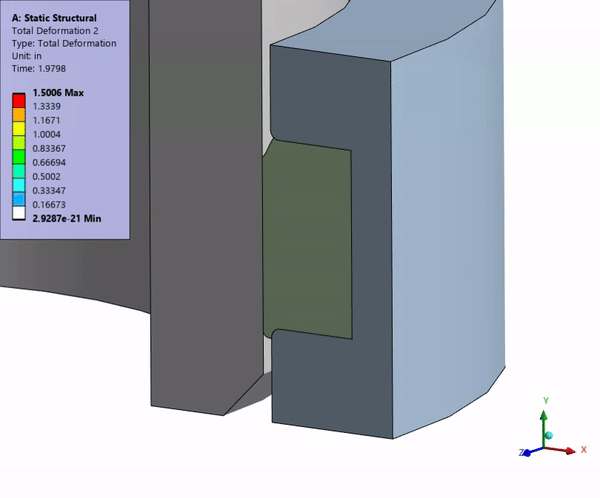
Modern Firearm and Ammunition Development Challenges
The development of modern firearms and ammunition presents significant challenges. Engineers must balance performance, reliability, and safety while keeping costs and production efficiency in check. Traditional methods rely heavily on physical prototyping, which can be time-consuming and expensive. Additionally, factors such as barrel dynamics, bullet drag, thermal effects, and recoil must be optimized to ensure a firearm function effectively under various conditions.
Accuracy is one of the most critical factors in firearm performance. Barrel vibrations, thermal expansion, and rifling design all influence how precisely a bullet reaches its target. Likewise, excessive recoil can reduce shooter comfort and control, while poor thermal management in high-rate firing scenarios can cause overheating, leading to component degradation or even catastrophic failures. Understanding and mitigating these issues is essential for advancing firearm technology. This blog explores the role of physics-based simulation in firearm development and how it contributes to cutting-edge advancements in the industry.
To dive deeper into these challenges and explore solutions, join our exclusive webinar and watch our in-depth video demonstration on firearm simulation techniques.
What is Physics-Based Simulation?
Physics-based simulation involves four critical steps:
- Providing CAD Geometry – Creating a digital model of the firearm or ammunition component.
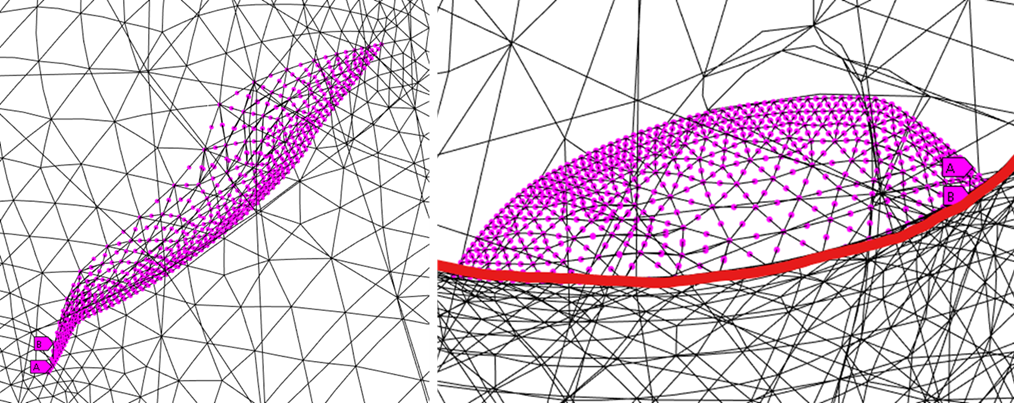
- Generating a Computational Mesh – Breaking down the model into smaller elements for analysis.
- Setting Up Physics Parameters – Incorporating factors such as sliding friction, pressure, heat transfer, and material properties.
- Post-Processing Results – Analyzing the simulation output to make simulation-driven design decisions.
Each type of physics—mechanical, fluid dynamics, and electromagnetics—has its own set of constitutive equations, allowing for quantitative predictions of firearm behavior.
The Role of Simulation in Firearm Development
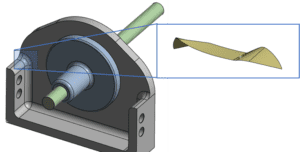
Engineers can conduct virtual prototyping and design verification, accelerating the product development process. Simulation helps solve fundamental laws of physics, including mass, momentum, and force balances, providing insights that enhance accuracy, durability, and safety. The following are key applications of Ansys in firearm engineering.
- Barrel Dynamics and Accuracy

Barrel dynamics significantly impact firearm accuracy. Simulation enables engineers to tune barrel dynamics by analyzing vibrations and harmonic frequencies, ensuring minimal muzzle movement.
- Bullet Drag Prediction and Optimization

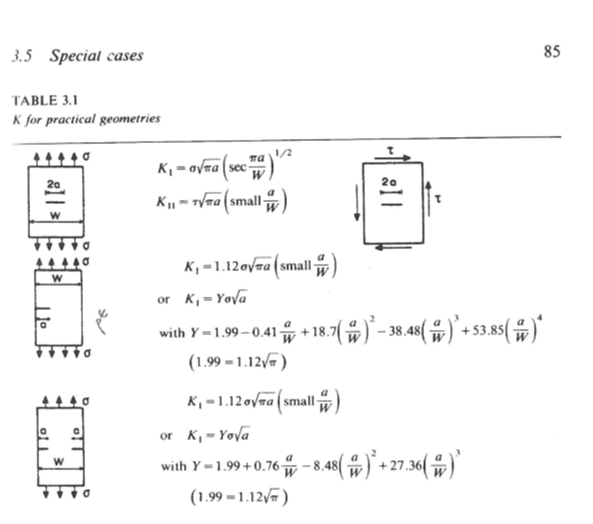
Predicting aerodynamic drag is crucial for improving projectile performance. Ansys simulations analyze bullet shape, rifling effects, and gas dynamics to minimize drag and enhance accuracy. By optimizing groove length and depth, engineers can achieve better flight stability and range.
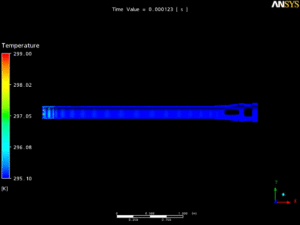
- Thermal Management for High Firing Rates

Excessive heat buildup in barrels and suppressors can lead to safety risks, including accidental cook-off. Ansys simulations evaluate thermal distribution in rapid-fire scenarios, helping to mitigate overheating and structural deformation. Thermodynamics, such as non-uniform barrel heating, can also be assessed to optimize material selection and structural integrity.
- Reducing and Predicting Felt Recoil
Recoil affects shooter comfort and accuracy. Simulation allows for ergonomic analysis, studying the effects of force distribution, action delay, and muzzle devices like barrel porting or brakes to reduce perceived recoil.
- Suppressor and Muzzle Blast Characterization

Suppressors are designed to dissipate pressure waves and reduce noise. Ansys simulations predict gas expansion and pressure variations, optimizing suppressor efficiency while maintaining firearm performance.
- Functional Testing
Mechanical components such as triggers, bolts, and actions require precise tolerances for smooth operation. Simulations assess tolerance stacking, material properties, and wear characteristics to ensure reliable firearm functionality before physical prototyping.
- Ballistics and Body Armor
Simulation plays a key role in assessing bullet impact on composite armor. Engineers can analyze penetration power, velocity requirements, and material resistance to improve both ammunition and protective gear designs.
Conclusion
Ansys simulation tools provide a competitive edge in firearm development by enabling precise, simulation-driven design optimizations. From improving accuracy and durability to reducing recoil and optimizing thermal management, physics-based simulations empower engineers to push the boundaries of firearm innovation. As technology continues to evolve, simulation-driven development will remain at the forefront of the industry, ensuring safer and more effective weapon systems for the future.
Want to see these simulations in action? Our webinar and video dives deep on firearm development with Ansys.